TK Test Kitchen

Post Sprint Debriefing for a few Simple Games created with Python's Tkinter


Quick Links

Tic Tac Toe
as it sounds

Proximity
a simple Mine Sweeper clone

Risk It
the main event
a territory capture game


All Code on Page
in native Python format
in one easy download

A Short Intro

I find that writing about my projects helps motivate me to finish them, so that's pretty much the why and wherefores of this page.

The stated goal of this particular group of projects was to get a handle on Tkinter (for Python, I pretty much only program in Python these days) so that I could create real-time interactive environments for any future project. And in regards to that, I would have to say Mission Accomplished! Forgive me if a dance and sing a little.

Basic Widgets

The code below (in text form, but valid Python otherwise) will create a widget that cohesively resizes. It's a little detail that's important to me, gives a bit of polish to the boards that follow... or, you know, after testing the projects again, I realize the Tic-Tac-Toe board doesn't actually resize and thus, my dissatisfaction with that is why the later projects actually resize.

Dynamic Resizing: basic code to get a resizing widget to screen. Doesn't do anything else.

In truth, the resizing code seems needlessly complicated to me (i.e. contains a lot of boilerplate). Alas, I am but a TK newbie. Who knows what I'm doing wrong?

Serving Python

Hosting raw .py files can be confusing to a server, as it's ambiguous whether to run or serve the code. Is it data or an application? Changing the extension from .py to .txt solves this problem, as .txt is always data (and therefor, viewable in the browser). In all other ways, the .txt code is functional.

The zip link at the top of the page contains raw .py files, which have been zipped (another way to bypass server confusion).

Lastly, I run all my Python inside Eclipse with PyDev (an IDE), so all the cruft that might otherwise be required at the start of a Python program is missing (i.e. no #! bin/python or however that goes, see, I don't even know), and there is no need for any convoluted command line argument parsing.


Tic Tac Toe

Screenshot of my implementation of Tic Tac Toe

Tic Tac Toe
code

Above, for your amusement, general edification, and/or reasons that only you could fanthom, please allow me to present a screen shot and link to the code for what I believe is a very nice implementation of Tic Tac Toe. Actually, outside of a few cosmetic changes to the code (one function is a bit messy to my eye), the only thing that really needs doing is implementing the dynamic resizing. But as I've already covered that in the previous section, I can't be bothered to make that change now. Thus, as with all good tutorials, I will leave that as an exercise for the reader.

For, there are other things I'd rather discuss at this juncture: you know, what have I learned, what would I do differently, and what am I still proud of in regards to this project... or something like that. Heck, truth is, sometimes, I just for the feel like to ramble the on, so please indulge me... or not, as is your pleasure.

Extreme Programming

At different times, at different moments in a programmers development, different ideas take root and have greater meaning. Or as they say, when the student is ready, the teacher will come. So, perhaps, when the programmer is ready, the paradigm will follow.

I take Extreme Programming to be the desire (and/or implementation of that desire) to restructure code so that comments are no longer required and are made superfluous. The easiest example of this is in variable naming:
Or if that's not clear, whenever I as the programmer forget what a variable does, that's a pretty good sign the name is in need of some serious refactoring.

Another example, found not so much in this program, but further down the page in the Risk-It code, I felt the need to break a class up into functional areas by inserting big comment blocks.

#######################################
      # # #    comments    # # #       
#######################################
Now, like I said, I put those comment lines in there to highlight the shifting focus of the class. But in truth, that's probably exactly where I should have broken up the class instead.

Anyhow, that's my take on Extreme Programming: comments are a code smell. Oh, I'm all for doubling down (please see above wherein I mention a willingness to ramble on, so commenting code is not a problem), but if the only way the code makes sense is with the comments, then I feel, that's a good indication of where the code can be improved.

Write Functions In Call Order

This probably goes against all sorts of design guides, but I don't care.

def play_turn_hard(self):
    '''Not worried about the extra loops,
    if/then guards makes the logic needlessly complicated.
    
    All play_'s yield None or a game_square number,
        so maybe's essentially.'''
    
    #in order of preference
    play_strategy = [
        self.play_first_turn(),   
        self.play_winning_move(),
        self.play_block_winning_move(),
        self.play_fork(),
        self.play_block_fork(),
        self.play_center(),
        self.play_opposite_corner(),
        self.play_any_corner(),
        self.play_turn_random()  
        ]
    
    plays = [play for play in play_strategy
        if play != None]
    play = plays.pop(0)
    #print play, play_strategy #yields a nice debugging string
    return play
I could pretty that code up (and maybe just reduce it to the pink area), but where's the fun in that? Besides, the extraneous print statement (in green) tells a story all on it's own: Python 2... and that play and play_strategy are what I care about in this function.

Anyhow, kibitzing aside, these nine 'plays' combine to make a winning Tic Tac Toe strategy. They are only called from within this organizing method. Hence, in the code, they follow this method in order. If I've ever gotten anything from the phrase Literate Programming, it's this: code as you would read.

Maybe

The above play's are all Maybe's as in maybe they have an integer value (the number of the square this strategic method recommends) or maybe the value is None (as in, this strategy yields no advice for the current board layout).

I was really pleased with the Maybe structure in this code. But, I'll temper that by saying, by the time I was finished with Risk It, I'd factored every last None out of that particular program.

There is Maybe (get it?) a happy place in between all or None... or more than likely, different problems require different solution sets.

Button Closures

I will end my commentary on the Tic Tac Toe game by noting that having little experience with Tkinter, I wrapped my on_click button commands in closures. What I should have done was use bind in lieu of command.

The truth is, the more I code, the more I'm coming to believe in the truth of the myth of the 10X Programmer. It's unlikely I will ever make this particular mistake again. And, well, they do seem to add up.

One last comment on closures, and likely why I brought it up in the first place, I don't really like closures. I don't think in terms of closures. So, along with comments, I'm going to consider them a bit of code smell. In this case, they solved the problem and allowed me to move forward quickly. But long run, it simply wasn't the best solution.

Known Solution

I like to believe the above covers what I learned; or at least, enough of the process that others might benefit... or if nothing else (and truly all I can measure), it definitely serves the purpose of a personal debriefing , the reason for which this page was ultimately created. So, the only thing left to mention is that the reason I coded Tic Tac Toe in the first place was because it was the first thing that came to mind after deciding to do a Tk project. Oh, that will be easy, I thought. And it was for the most, just a couple of hickups in the game logic. But as it was a solved problem, there was plenty of help out there. And for the most, that's why I picked a Mine Sweeper clone for my next Tk project. Something simple, on the assumption most of the new stuff (new for me, anyway) would be in the Tk Interface, itself.


Proximity Fuse

a.k.a. yet another Mine Sweeper clone

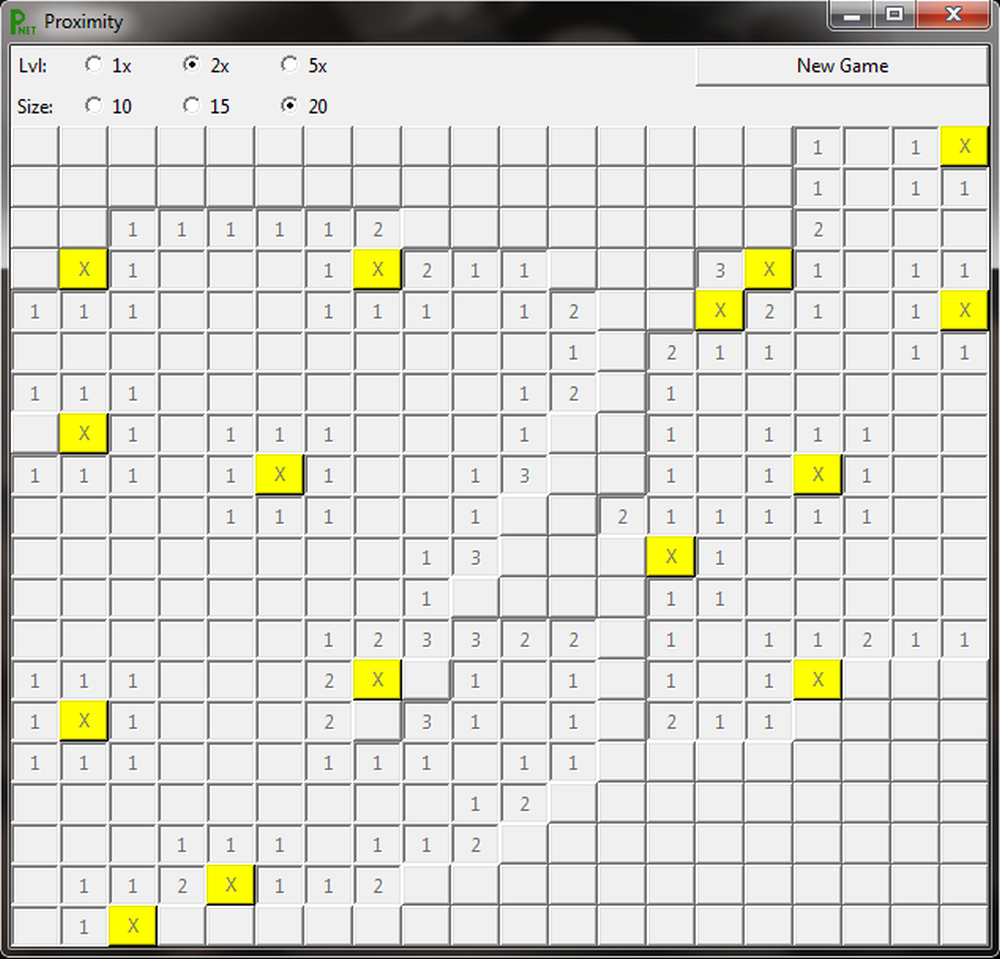
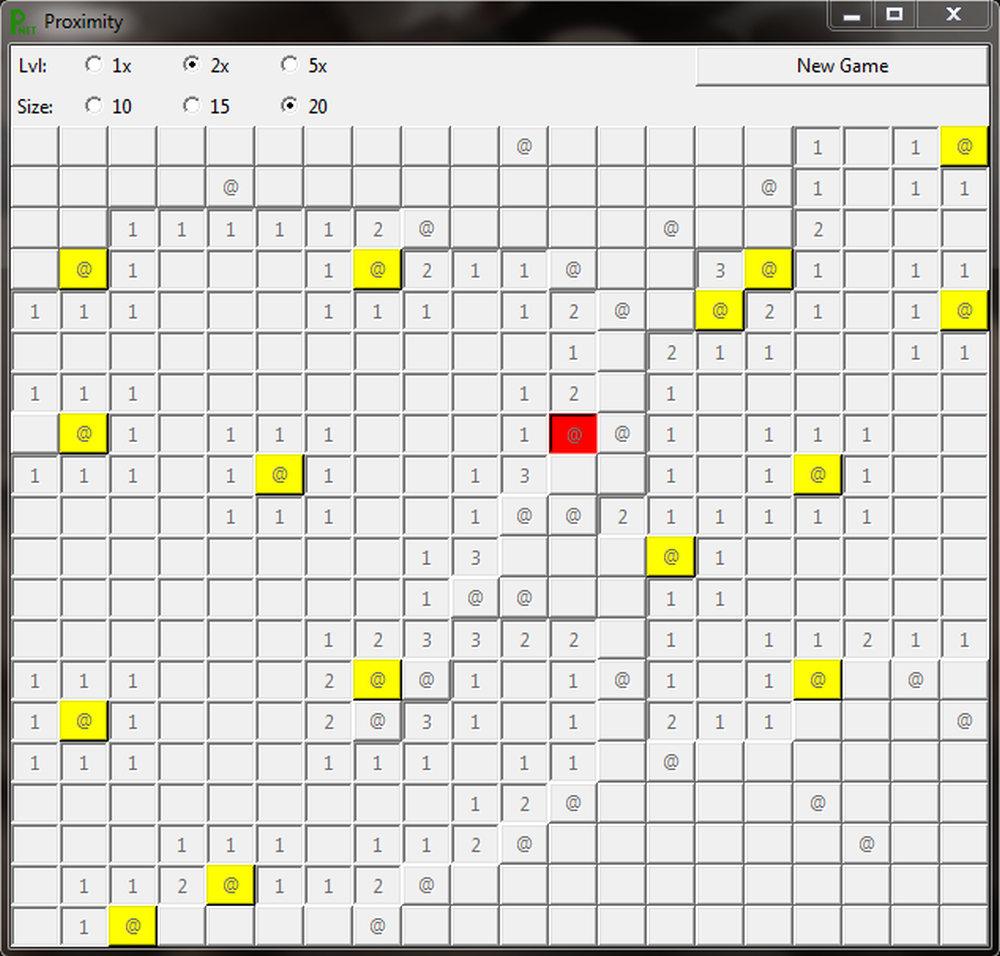
Screenshot of Proximity, my implementation of Mine Sweeper, showing game in progress, yeah, the highlighted red x in the upper right corner on this one, but not on the next bothers me, but not so much I'm going to replay it, not at the moment, at least Screenshot of Proximity, my implementation of Mine Sweeper, showing the loosing state

Proximity
code

Wow! You know, I'm actually kind of surprised that after refactoring the code, I don't have much of anything to say. Oh, it's not perfect code, but what would I tell a past or future version of myself?

I like playing this game.

It bothers me that the highlighted red closing 'x' that appears in the left hand image above doesn't appear in the right hand one (this having nothing to do with coding or the red @ in the game, but rather, my ability - or rather, inability - to take consistent screen shots). But it doesn't bother me enough to fix it... especially after writing an explanatory comment like this (own your mistakes, my friends). In fact, after making the Game Play images for the next section (you'll see, they're uneven), perhaps the simple truth is that I'm doing something wrong (screen shots, suck at, taking, I do). Oh, well. That's not really what the page is about, so I'm just going to move on.

Heck. Maybe I'm just anxious to get on with the main event.


Risk It

A Short Preamble

The first thing I'll say, is that when I work on a project that I know (just know) I'm going to turn into a major webpage, I stock up on the Work In Progress: 20,000+ images, taking up 250+MB in this particular instance (along with code saves, log files, etc.). Though to be fair, the vast bulk came from saving every turn as an image in a thousand game tournament. Eh, silly thing to do. Still, I did it...

And as you'll see from what follows, I totally did not over-estimate my needs. Or, sarcasm aside, it's much easier to over save, than go back and recreate state. Besides, most of the temporary files will disappear within the week... or at least, I hope. I'd really like to wrap this up soon. Going on two months, I want to get this off my desk (and out of my mind). Time to move on...

Tkinter Implementation

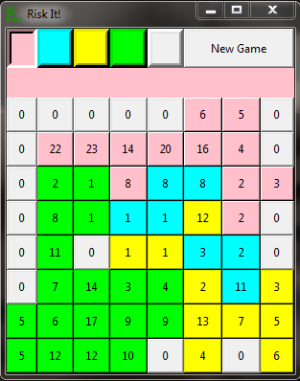
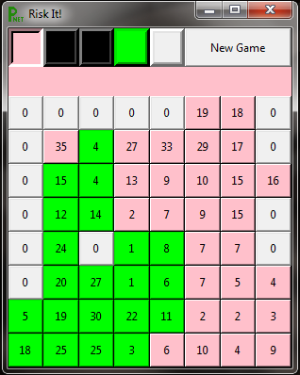
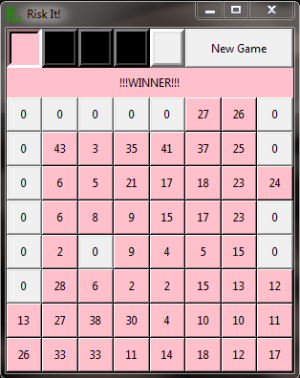
First turn of risk it play, i am pink mid way in the game after I elminated blue and yellow me winning it all, opponents playing random
- - unequal heights, the images, they are - -


Risk It
Tk code

Game Play

I have absolutely no intention of going back and changing, updating, or refining anything about this game, any more. That said, I did just notice when playing the Tk version (to grab the screen shots, don't you know), I implemented the surrender condition differently than in the Logic version. On surrender, in the Tk version, the attacker gets all of the defender's units. In the Logic version, units on all newly taken over squares are reset to one. I don't think this would have much effect on the logical analysis that follows, except that resetting the units to one, likely creates longer games.

But the main point is, I made a mistake and some of my analysing data might be off (so don't base your PhD thesis on it). I shall now hang my head in shame.

1...
2...
3...

OK, that's about all the shame I have in me. Time to move on.


Logic Implementation

Game State Every Fifth Turn
Left to Right, Top to Bottom

this is the only alt for this lot, as follows is the sample output for a Risk It game, every five turns or so, snapshop
And pink wins!

Risk It
logic code

Sum over Product

I started with a few rough ideas; but for the most, game play came together dynamically (on the spur of the moment) while coding the Tk interface. Or in other words, I had a general sort of idea, but all specifics were decided on the fly: colors, size of board, starting positions, surrender dynamics, and battle resolution.

As to the surrender dynamics, I've already discussed the captured unit discrepancy between the Tk and Numpy version (in Tk, units = 1 on takeover; whereas, in Numpy, they are unchanged).

This next item isn't so much a discrepancy, as a change in design. Originally, I had coded the die roll value as being a product of the number of dice, but I didn't like the spread that gave:
Given no zeroes, the average value of 50d10:
    sum = 250
    product = pow(5, 50) #a much larger number
So, I refactored the die roll mechanic:
rolls = [randint(0, 9) for _ in range(units)]

#Original Version
total = product(rolls)

#Revised
total = 0 if 0 in rolls else sum(rolls)
And that gives us the graphs as shown below.

Average Roll
5 * num_units

In the final graph, black is expected value by simple sum, while red takes zero rolls into account; thus the black area between the green and yellow lines represents the total average roll after taking zeros into account (i.e. larger unit stacks roll a lot more zeroes, but when they don't, they achieve higher results).

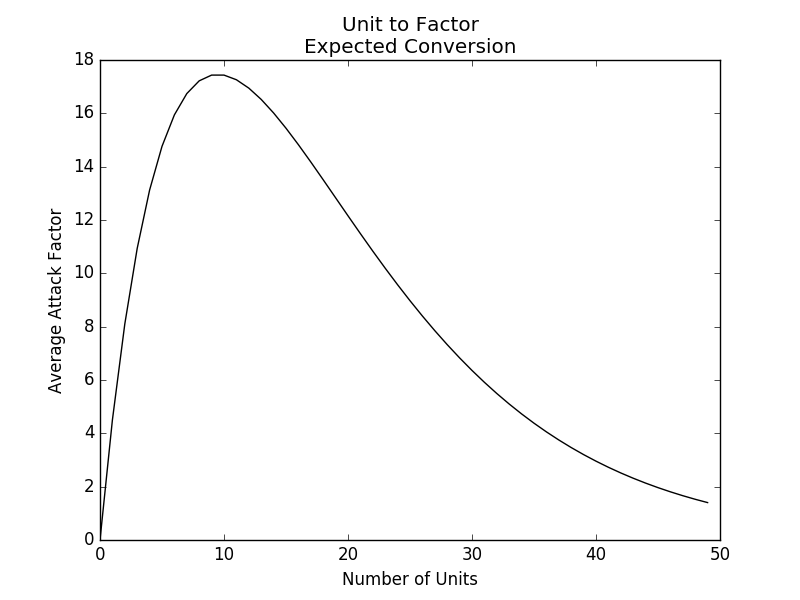
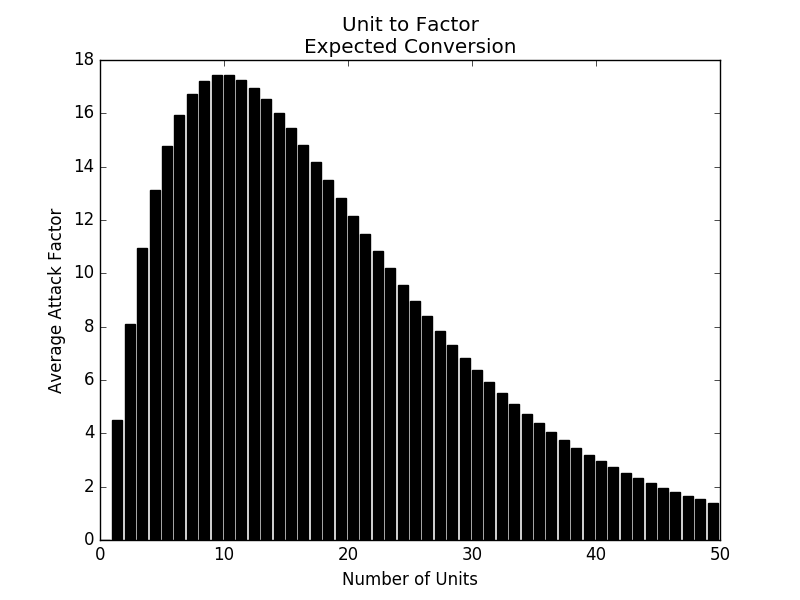
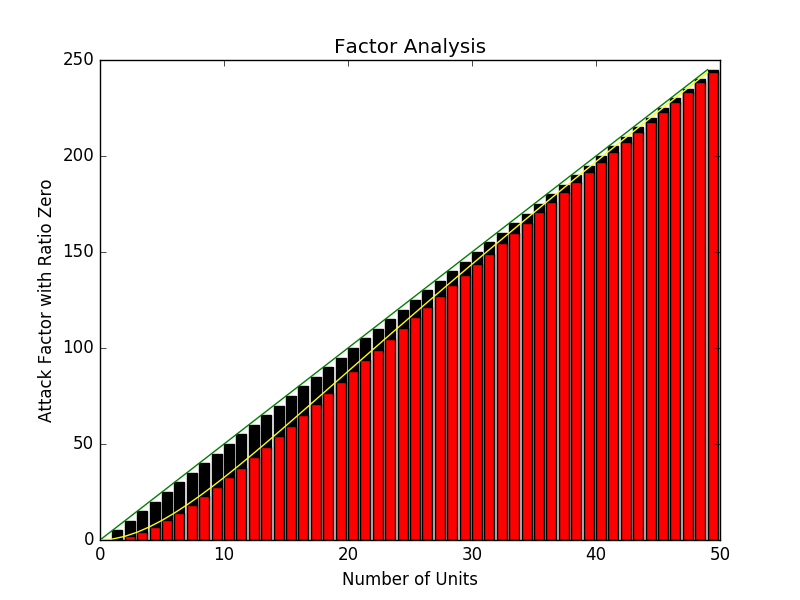line graph showing expected value of rolls for given unit stacks bar graph of same thing detail showing where the average comes from, total expeted roll of five times dice times probability of no zeroes
Perhaps math is just not my thing. I seem to be having a harder time explaining this than I would have expected. Ah, it's probably because I don't have good variable names.
d10_ave = 5
    i.e. sum(range(10)) / 10 = 5 

chance_no_zero = 1.0 - pow(0.9, num_dice)

def ave_roll(num_units):
    factor = 5 * num_units * chance_no_zero
    return factor
So, the first and second graphs are line and bar graphs of ave_roll, while the final graph tries to explain the rationale for why that is so. Have I succeeded? I mean, I could keep on going, but it's probably not important. Just take my word that by using sum (instead of product), it's, now, possible for a smaller stack of units to win against a slightly larger one even if neither rolls a zero, while the built in disadvantage for extremely large unit stacks is maintained.

I don't know. On one hand, it seems like a trivial thing to discuss in so much depth. But on the other hand, item by item, it's all trivial. Seriously, no one aspect of programming is difficult; it's putting it all together that's proves challenging.

Factor Analysis

In many ways, the following is at the heart of the strategic logic for my system, but in others, it's been pushed to the side. Truthfully, if I had to do it over, I wouldn't bother with arrays.



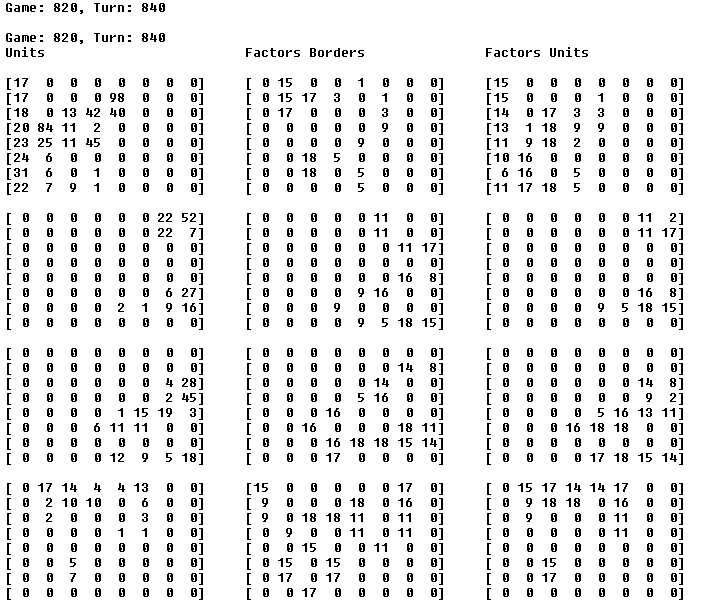
For most of Risk It's progression, I used a three dimension stack of arrays to represent the game field, which is to say, there was an 8x8 game field for each of the four players. In the final version, I inserted the neutral squares at the 0 level, which made truth testing easy: 
if player:
    then

# True for players 1-4
# False for neutral, player 0
I had been using players 0-3 with None for the neutrals, but that had a subtle bug to it, as the player in the first layer of the array (i.e. Player #0), tested just as False as a None did. And by bug, for the most, I mean, I had a hard time keeping it all straight.

Anyway, that all feels a bit obscure to me, so let's move on.

The above represents a numerical array of the game board. The first column, Units, is number of units a player has on a square. Factors Borders represents the attack value (the average expected roll) those units might exert on uncontrolled neighbouring squares (i.e. squares that don't contain any of that player's units). While, Factor Units, in the final column, represents the attack value of the units, where the units stand.

It's a nice sort of visualization. I am proud to be sharing it with you. And yeah, I think it would have been quite beautiful to arrive at the correct attack by some sort of array shifting manipulation...

game play state, unit squares game play state, factors, squares units could attack for pink factors, blue factors, blue factors, blue
Far Left: Unit Game State
Followed By: Factors, squares those units could attack


But ultimately, I created an Attack class, that superseded the above and made it completely unnecessary.
class Attack():
    '''Used to store each individual attack possibility.
    All possible attacks are computed every turn.
    However, scoring is only done for advanced play.'''
    
    def __init__(self,
        row_att, col_att, row_def, col_def, defender, score=0):
            
        self.row_att = row_att
        self.col_att = col_att
        self.row_def = row_def
        self.col_def = col_def
        self.defender = defender
        self.score = score
Attack.score is the key attribute here. Want to know the easy way to solve the problem of the best move in a game like this? Create a list of all possible moves (attacks, whatever you want to call them), score them by some metric, sort, and take the best. Problem solved. And actually, an even more complex problem is solved for free at the same time.

Skill Level

I did not implement skill levels in Risk It. But in my next project, I likely will. Here's the psuedo code. I can't imagine the real code would be that much more complicated:
attacks = [Attack(), Attack(), ...]
attacks = sorted(attacks,
    key=lambda attack: attack.score, reverse=True)
	
size_slice = len(attacks) * skill_level
attacks = attacks[:size_slice]

final_attack = random.choice(attacks)
If that seems complicated, let me break it down for you. List all attacks, score, sort, take the n best attacks (n being determined by skill level), and select one of those attacks at random. That's your attack.

Strategy

The evolution of the Logic module was not linear. I didn't decide that creating an Attack() class was the correct solution until almost the end (see, all that time a 10x'er wouldn't waste). So, it's not like, Oh, well, with that out of the way, the only thing left was to implement the strategy.

What it is exactly like is Oh, well, with that out of the way, the only thing left to talk about is the final strategy and it's evolution.

To assist in analysing strategy improvements, I made a Tournament Harness (or call it what you will; personally, I choose to call it a Tournament Harness) in which the computer would play a thousand back to back games against itself, while saving win results and so on. Snapshots of game state comprise most of the save files I mentioned earlier. Not knowing what I'd need or want for this page, I often kept an image showing state for every turn in every game for every tournament. This really added up; and in hindsight, was extraordinary overkill. Though, at times, it was very helpful to 'step through' the games visually to see what was happening during the play. But ultimately, since I'm not posting that many images, I didn't need to save them from tournament to tournament. All I really needed (looking back, hindsight 20/20 and all that) was a .csv text file that advised of the state when each of the three losing players was knocked out (first and last game in each of the thousand game tournaments shown).
#First Game in Tournament
0,9,1,9,5,1,4
0,9,2,4,3,1,4
0,9,3,4,3,1,4
0,54,1,131,21,1,3
0,54,2,48,8,1,3
0,56,1,159,29,1,2


#Last Game in Tournament
#  with newlines added for clarity

999,21,1,11,5,1,4
999,21,2,4,3,1,4
999,21,3,12,5,1,4

999,129,1,357,27,1,3
999,129,2,209,14,1,3

999,131,1,397,42,1,2
The columns in order are:
game_num
tournaments consist of 1000 games (0-999, with 0 and 999 shown)
turn_num
games themselves are of indeterminate length
player
1-4 (in this data, 0 is neutral, so can't win or be knocked out)
units
total number of units player owns
squares
total number of squares player controls
attacker
the saves are triggered by a player being knocked out, the attacker is who did the 'knocking'
defender
the player is who was just knocked out (i.e. the third and last number are never the same for any turn group)
This is likely more detailed than anyone cares about. But this data is the sole basis for the following graphs, which form the main analysis of the AI's Strategic Evolution.

Random

Random is as Random sounds.

Using random input for trial runs or test data can be, um, problematic, as the output is non-deterministic; and therefore, not predictable. But I feel it was the way to go for a base-line strategy.

And in case that strategy is still unclear, in Random play, a player picks a move at random from all legal moves.
attack = random.choice(all_possible_attacks)
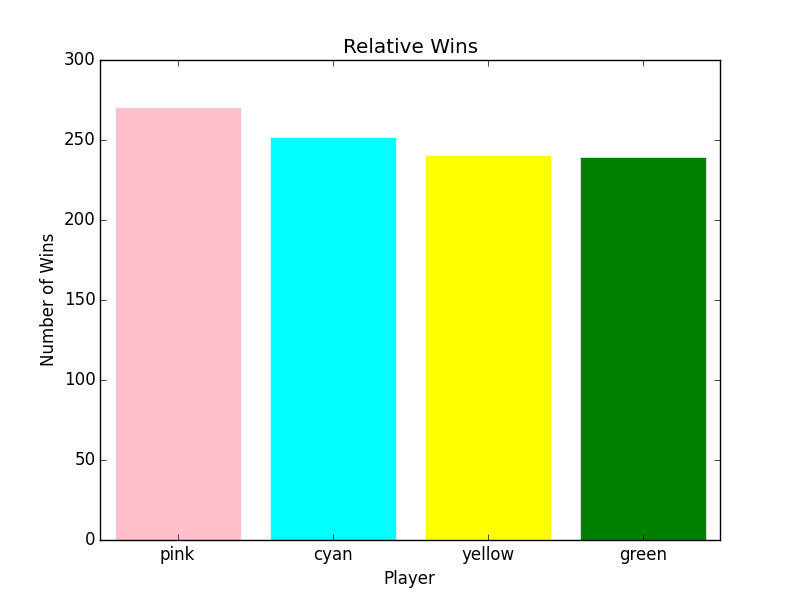
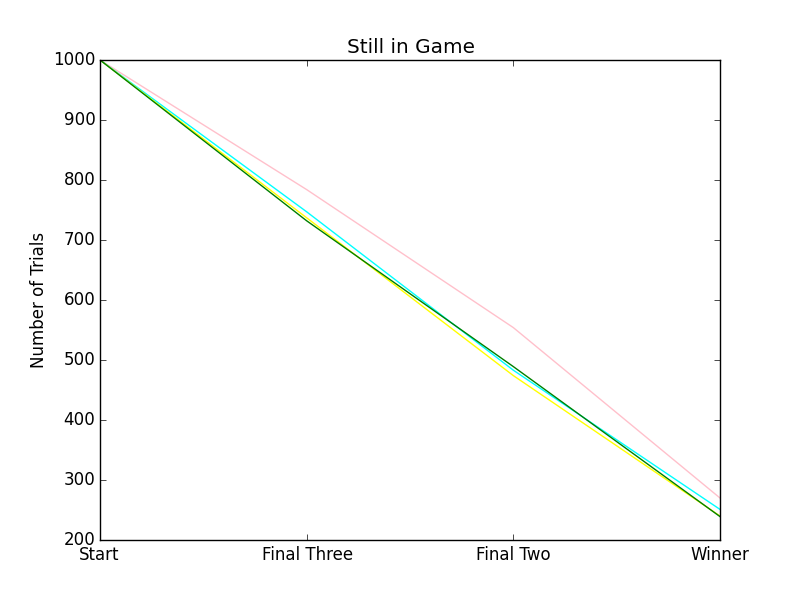
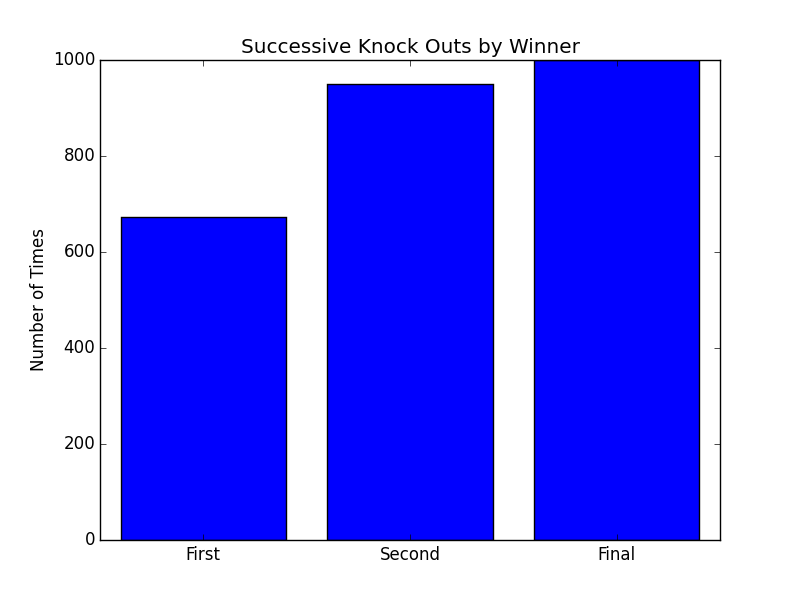
Relative Wins, Random, graph, see text, all bars are about equal at 250, random condition rank Order, when each player drops out, first to go, second, third, or winner, all are about equal, random condition three bars, does the eventual winner knock out the first or second player, they always knock out the third, that is what it takes to be the winner, random condition

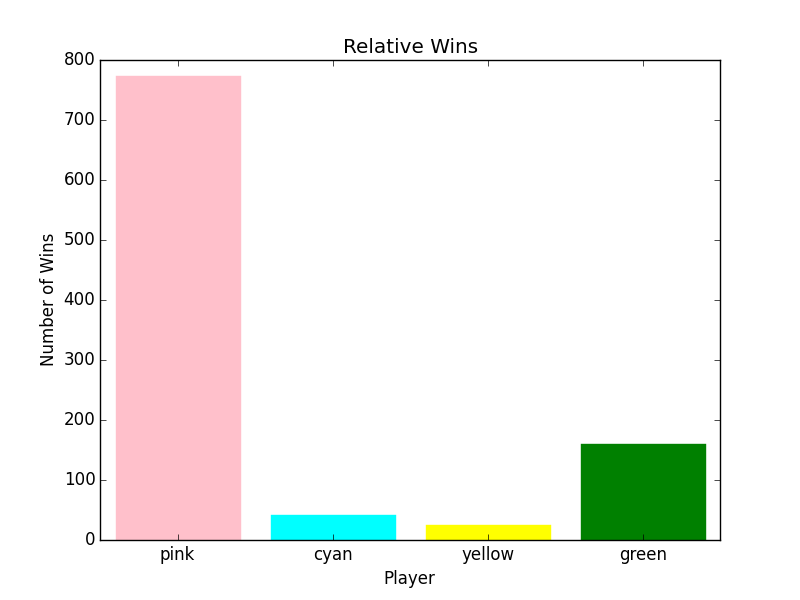
Pink has a slight advantage as it goes first; and so, is basically always one turn ahead. I didn't like the way these looked (didn't believe the results, pink shouldn't do that well), so I ran the tournament again, and got results more in line with an equal split. Still, I figured I'd post the slightly lopsided results, instead, as they are from the first tournament I ran.

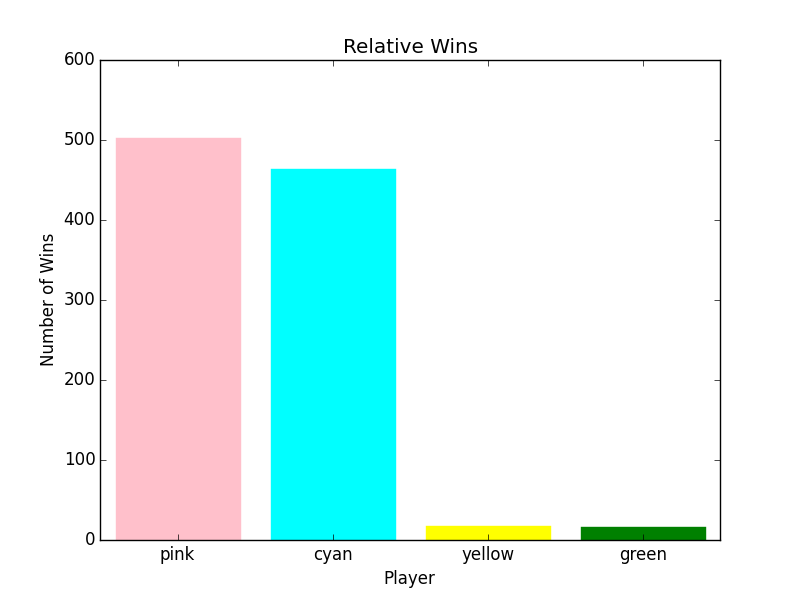
The First Graph, Relative Wins, shows how often each player wins, in this case, it's split pretty evenly. Any strategy that increases the relative number of wins is better in my book. It shall be the metric for deciding 'better'.

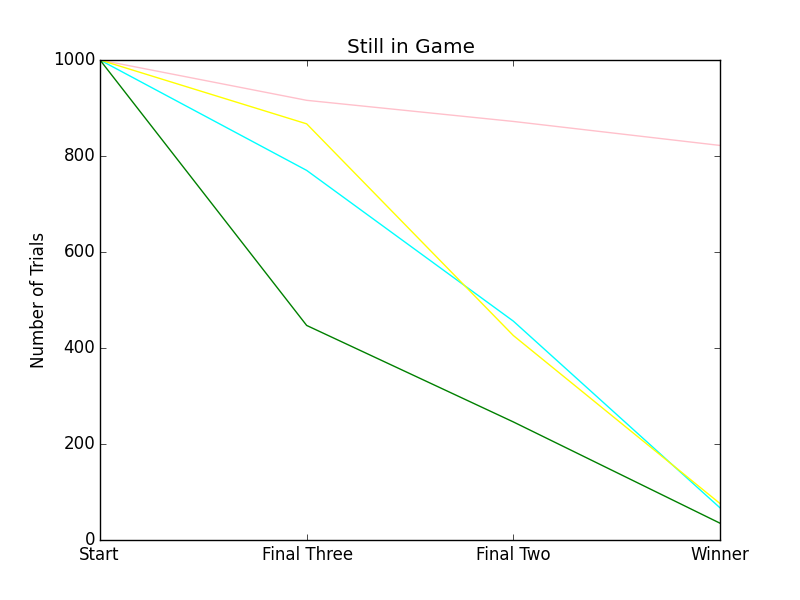
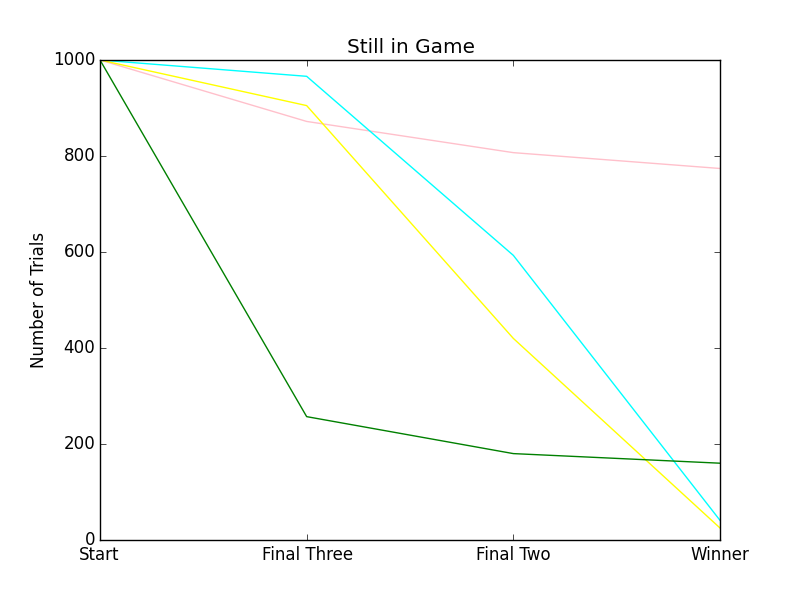
The Second Graph, Still in Game (a.k.a. Rank Order), shows average length of time a given player stays in the game (whether they came in first, second, third, or last place). The higher the line, the better the strategy. As all the lines are about the same above, it should be no surprise that one Random strategy is just about as good as any other Random strategy. There are only four data points to each line, so using lines for the graphs is as much about clarity as anything.

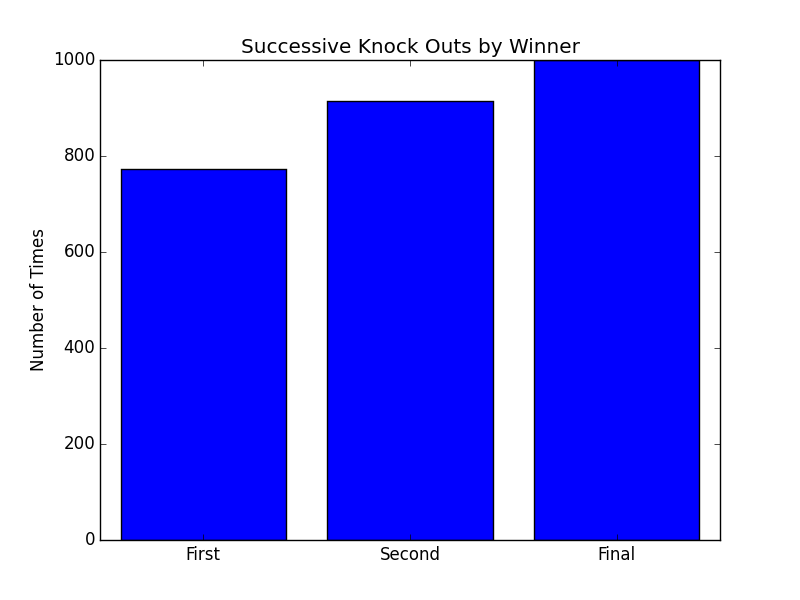
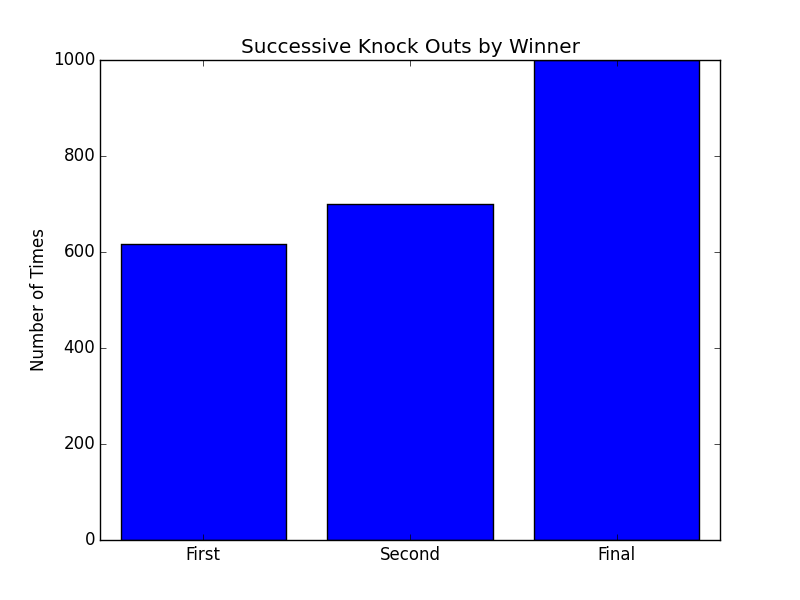
The Third Graph, Knock Outs, shows the relative frequency with which the ultimate winner eliminates the previous players (how often the winner was the player who knocked out the first, second, and third opponent from the game). Since the winner will always knock out the player who comes in second (or is the Final opponent to be knocked out), this number is 1000 for all graphs of this nature.

Being random, there's not much of a need for any analysis. The results are about as I expected. As mentioned, random data is not always such a good baseline, but I can't imagine anything else that would work in this particular case.

If interested, the graph point numbers (as opposed to the raw data) is saved as comments in the underlying html. Though, why exactly anyone would be interested... sometimes best not to think too hard.

The only additional analytical data I have is the average number of turns in a game. I didn't graph it. Maybe I should have. Whatever. In addition to posting average game length here, it's posted as a combined table for all the strategies, further along.
Game Length
Mean: 356.07
Std Dev: 246.11
Max: 2547
Min: 24

Circular

It's called Circular because the attacker preferentially attacks whoever is going to play next (though, in the final refactor, and hence, final set of graphs, that was changed to the highest number player). The essential feature in Circular is that a player using this strategy targets one other player and attacks them exclusively.
possible_attacks = [attack for attack in all_possible_attacks
    if attack.defender == targeted_player]
attack = random.choice(possible_attacks)
In the graphs that immediately follow, Pink targets the lowest numbered player it can reach. While in the final graphs where two players are using the Scoring Strategy, they both target the highest numbered player each of them can reach. So, one might target the other (giving an advantage to the lowered numbered player) or they might both target the same opponent (sucks to be Player #4).

Also, while I feel bogged down in the details of this change (Circular going from low to high in attack preference), I might as well mention that changes like this go a long way towards explaining all the data (images, code versions) I keep en-route. Reconstructing the past is hardly ever worth the effort, but there might be some key detail or insight in the change worth exploring. In this case, if we're going to be honest, it's slight at best. Though, in the earliest versions, I actually created a play-order list of the remaining players (selecting whoever was to play next). Let's just say, selecting the highest or lowest numbered opponent is much easier.

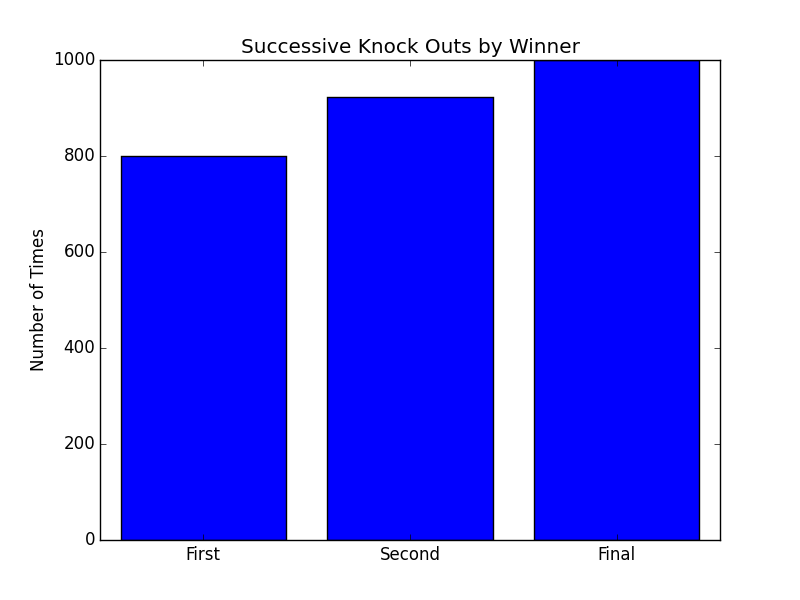
Anyway, that aside, below: pink targets cyan (light blue), yellow, and then green, which goes a long way towards explaining why cyan tends to get knocked out of the game first, yellow second, and green third.

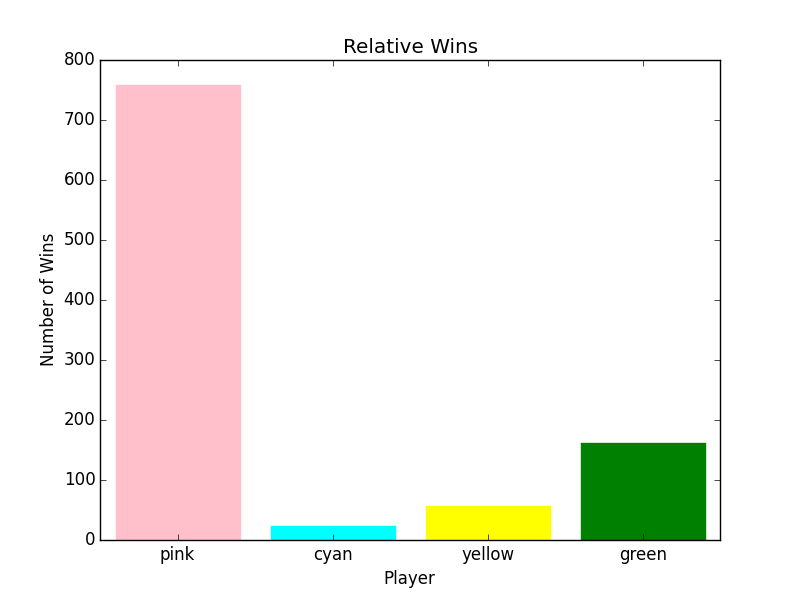
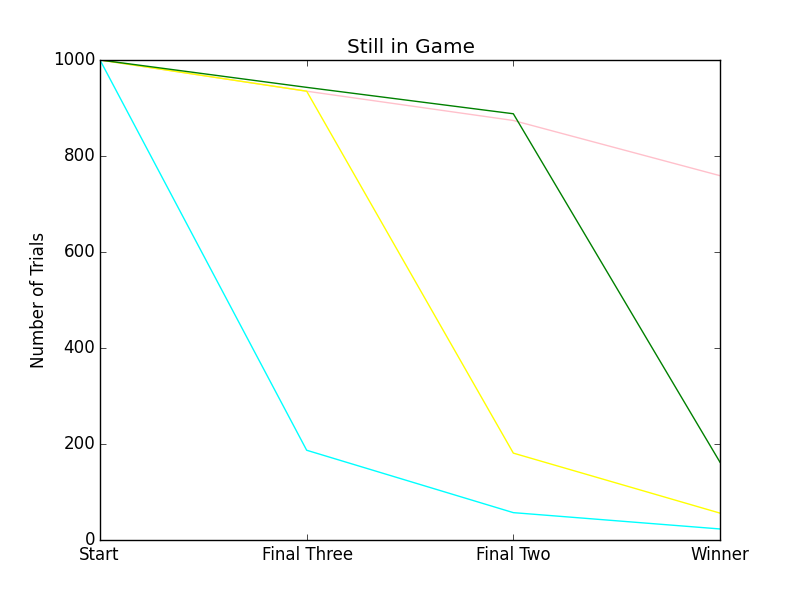
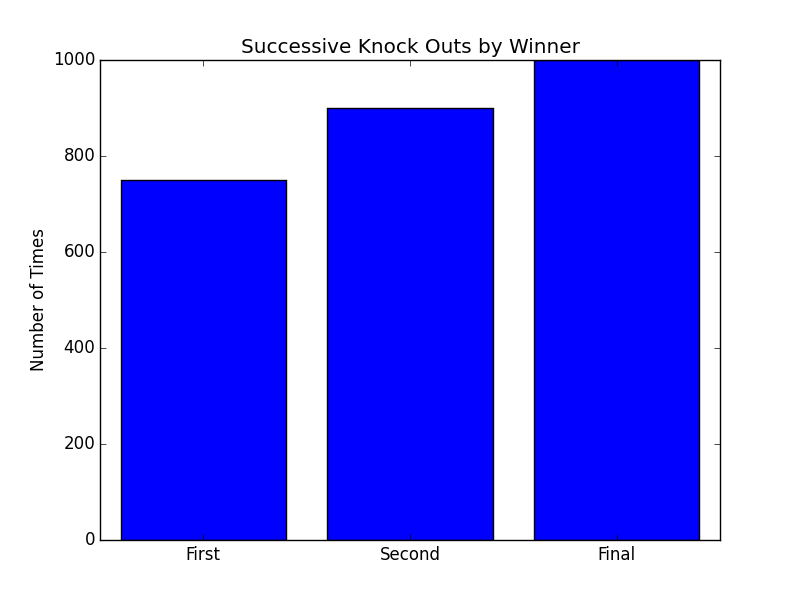
Relative Wins, Circular condition, pink trounces others, winning 700+ Order of elimination, pink clearly the best, green comes in an obvious second, green is the last player pink goes after typically, the winner knocks out the rest, but in 400 games someone else knocked out the first to be eliminated 
Game Length
Mean: 162.18
Std Dev: 126.93
Max: 1795
Min: 12

The Circular strategy upped the win percent from around 25% (even split) to about 75% for pink. The main reason for this is because Risk It includes cusp points: it is a possible for a player to cede all their squares to another player. Targeting the same player over and over, while the targeted player moves at random, increases the likelihood that the targeted player will ultimately surrender to the attacking player. And having other players surrender to you is key to winning the game.

Risk

I like Risk, which is sort of, kind of, not really, the inspiration for Risk It. Since any reader is likely to be much more familiar with Risk than Risk It (bloody shame, that), let me just say that if you know what you are doing, an average game of Risk with six players shouldn't last but ten turns (give or take a few, seven turn wins are common). You see, at the second card turn in, which happens at turn 6-8, the sole goal is to knock out another player; and if this happens, the attacking player gets all of the defeated player's cards, which if they now have more than five of, they must immediately turn in (hey, them be the rules); and by using the armies thus granted to knock out another player, well, the whole thing tends to steam roll and become unstoppable. Oddly, I've never played a computerize version of Risk (not that I've played that many) that took this cascade into account. I won't rant more about Risk. Suffice to say, it's not really a long game. Once one player starts knocking out the others, they tend to win.

I mention this only because Risk It has the same winner take all dynamic, which is what the blue bar graphs on the right are about. Whoever defeats the first opponent tends to win the game. Looking for a linchpin strategy in Risk It: win early and win often.

Best Attack by Score

I've mentioned how I hoard lots of data and images on the way towards making a web page. There were a lot of refinements between Circular and the final Scoring Strategy, which I'll summarize in a bit. But first let's look at the graphs.

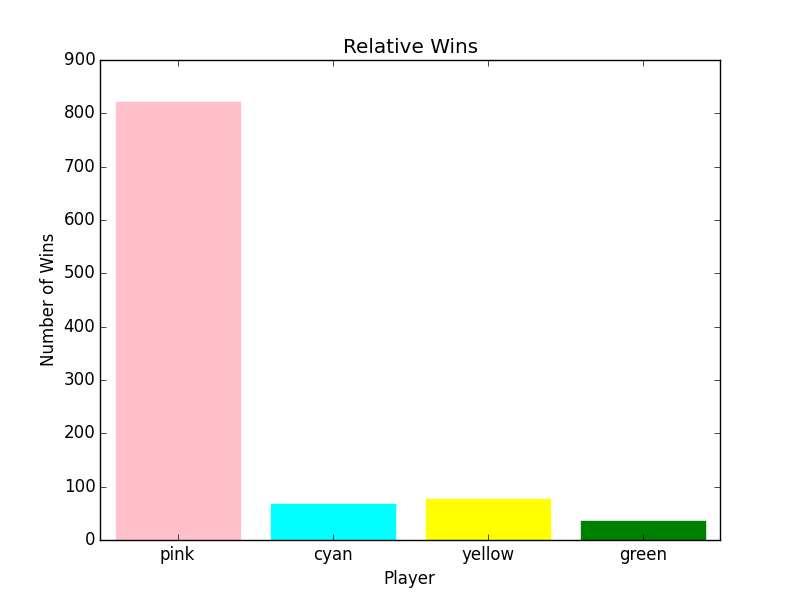
Relative Wins, Circular condition, pink trounces others, winning 700+ Order of elimination, pink clearly the best, green comes in an obvious second, green is the last player pink goes after typically, the winner knocks out the rest, but in 400 games someone else knocked out the first to be eliminated 
Game Length
Mean: 172.65
Std Dev: 150.51
Max: 862
Min: 15
Scoring is better, but not by that much: 
Strategy        Scoring   Circular
Number Wins       822       759 
Game Length       172       162
So, Scoring won more games, but Circular did it faster. Of course, far more importantly from a game play perspective, I imagine Scoring would seem fairer (as, lo to the human player, who the computer decides to target).

I've posted the code, so any who wants can see how the score value is computed. But it's probably not that interesting... or relevant, as the exact score value is dependent upon arbitrary weights that I simply did not try to optimize. However, the concept if fairly straightforward (written 'backwards' for clarity, so more math-like than code-like):
attack_value = defender_value + square_value

defender_value = surrender + def_units
    + def_squares + def_num
	
surrender = +25 if def_will_surrender else 0
def_units = defender_total_units_on_board
def_squares = num_defender_squares
def_num = 5 * player_number

square_value = factor_attacker - factor_defender
The above should be fairly self-explanatory. Two sub-scores make the total score: a score computed for each defender player and a score computed for each defending square. The defender_value is heavily weighted towards a player that is ready to surrender (remember the cascade), favours a defender with lots of units (because they might lose a lot of units in the attack, which in turn will push them into surrender mode), likes players who do not have many squares (i.e. who are weak), and has a high player number (so the reverse of the original Circular logic). Then there is a value for the specific attack, which is basically the attackers chance of winning (attackers_factor - defenders_factor). After computing a score for all_possible_attacks (all neighbouring squares), the Scoring Strategy simply chooses the highest valued attack as the final attack.

Coding this all took a lot of work, as I felt the need to do several refactors to implement the changes, and didn't give much better results than Circular. So in the end, it wasn't worth it. Still, at the time, it was one of those things that needed doing... as perhaps, does the next section (i.e. needed doing, being why I did it and/or being a case point example illustrating why my priorities are all out of whack).

Two Player

I could probably stop there (well, not me, but someone who had their priorities straight and not all out of whack could probably stop), but I've already gone to the bother of making a few more graphs, which show what happens when two players use the Scoring Strategy. So, I might as well post them.

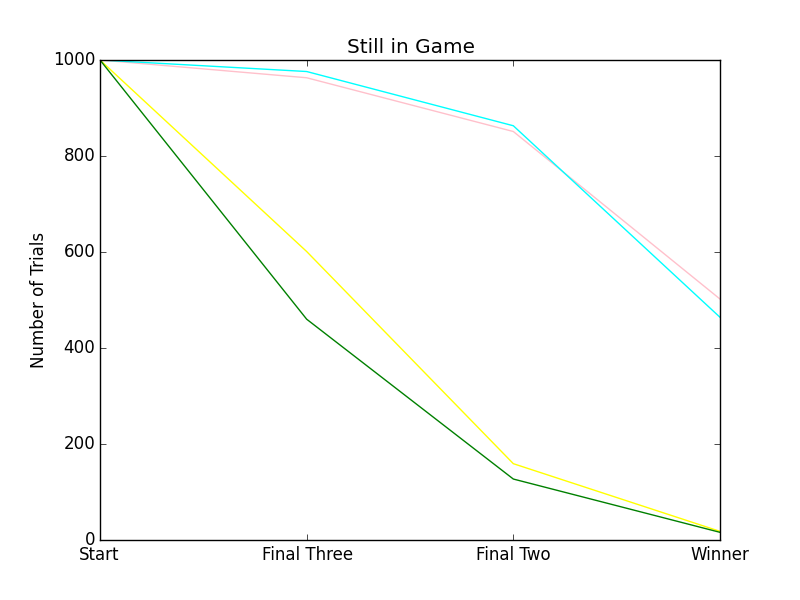
Final refactore, score logic, pink and cyan (1 and 2) playing with good logic, they split the win pink and cyans graphs overlap as to yellow and green the winner doesnt take out the first player as often
In the above, Player #1 and Player #2 (pink and cyan) collectively demolish Player #3 and Player #4 (green and yellow).

Final refactore, score logic, pink and green (1 and 4) playing with good logic, pink trounces, green distant second if green stays in the game, green typically wins the winner doesnt take out the first player as often
This is more or less the same, but with Player #1 and Player #4 (pink and green). Since pink pro-actively targets green, but green doesn't return the favour (targeting yellow instead), without looking at screen shots of the game (who has time for that, seriously), I'd say the only time green wins is when it eliminates yellow before pink does it's job. That's actually quite the trite statement (a.k.a. a truism), so let's reword it and instead say, sometimes green gets too powerful for pink to knock out no matter how hard pink tries.

Way to go, green! That'll show those Pinko Pink Players.

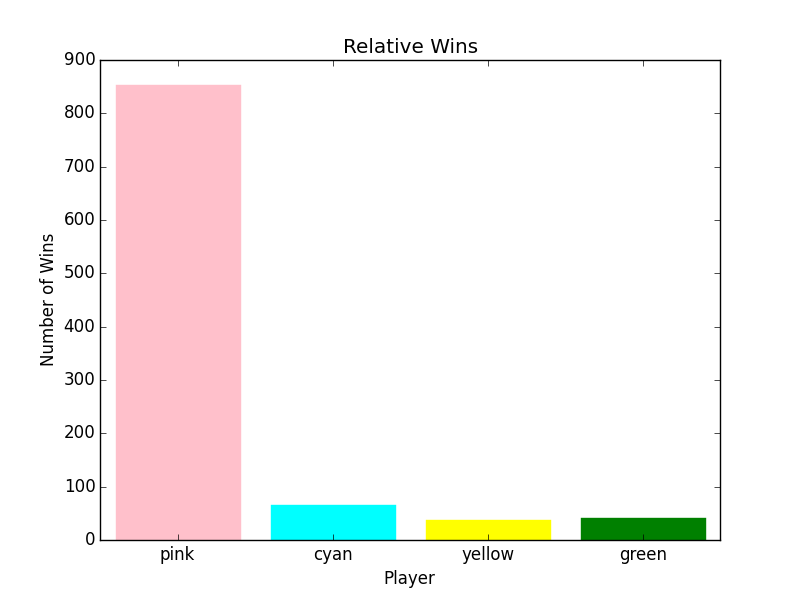
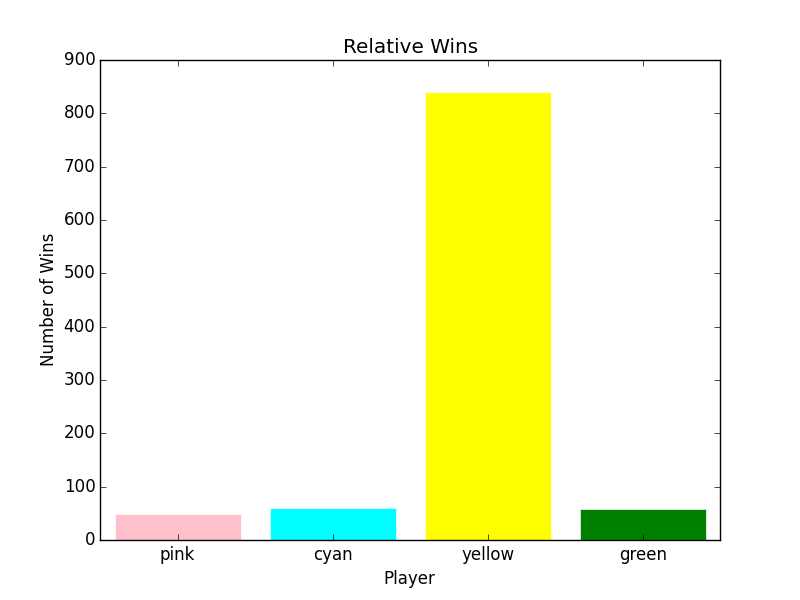
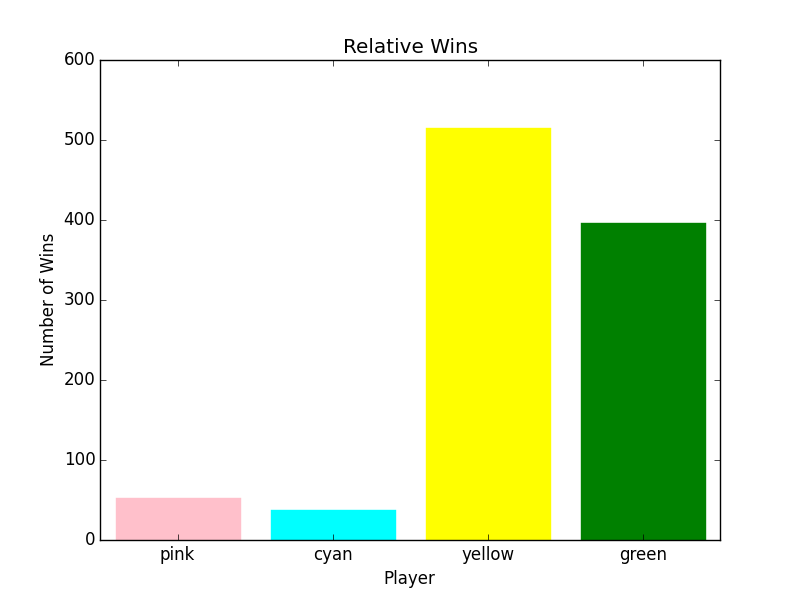
Final Logic, Pink Trounces all Comers Yellow is playing the scoring logic and wins decicively, just like pink did before yellow green, split, but yellow ahead of the game, I attribute this to preferential attacks against higher number players

These are the final three graphs. (Yep, I scrolled down just to make sure. They are the last.) They show pink only using the Scoring Strategy, then only yellow, and finally yellow and green. I used a weighted preference for attacking the higher number players (5 * player_number), so that (I hope) explains yellow winning more often. Yeah, sure, yellow targets green and green targets yellow (both going for the highest numbered opponent), but yellow goes after green more that green goes after yellow.

Once again, if this wasn't the end of the road, that might be something to dig into deeper. Is my analysis correct? Is it a bug? Or is some other mechanism in play? The world may never know.

Below (and as promised), a handy table presenting the data for turn length and win ratio for all the graph series presented.

       Pink   Yell   Pk/Cy  Pk/Gr  Yw/Gr  Rand  Circ
Turns           
Mean:  200    299    200    256    419    356    162
Std:   248    279    248    690    858    246    126
Max:   1788   2021   1788   8918   9000   2547   1795
Min:   16     20     16     21     26     24     12

Winner
P-0    854    46     854    774    52     270    759
P-1    66     59     66     41     37     251    23
P-2    38     838    38     25     515    240    56
P-3    42     57     42     160    396    239    162
The truth is, I probably care more about aligning those numbers all nice and pretty than anyone reading this page will likely ever care about what those numbers mean.

Still, what do those numbers mean?
Truthfully, I find those outlier game lengths to be interesting. If I were to probe deeper into this project, I'd like to understand the reason for those long game lengths (and not just guess the computer got locked into a relatively even mid-game draw).

Alas, for the most, this is the end of the line for this foray into Tk.

In fact, at this point, the foray is soooo over. So over, I don't have much to say about hooking the Numpy Logical implementation back into the Tk version. All of these projects (Tic Tac Toe, Proximity, Risk It) started as Tkinter Test Projects. But this last, really reverted to a Numpy one. I am very familiar (well, comfortable enough) with Numpy. And in truth, if I were to make this game again, I'd start with Numpy, code it all out, and make the Tkinter presentation layer last. That just might be my own personal bias. I know Numpy, while Tkinter is new to me, so guess which one I'm more comfortable in. But possible subjective bias aside, I think it would be cleaner to work out the Logic first and then implement the GUI, rather than the other way around. Much like someone might be better off writing the text for a post prior to worrying too much about the presentation of said text. Of course, having said that, I must admit that I never write anything without thinking about the presentation, so...

Eh, at this point, I really am bleeding over into the last section, so I might as well start that now and be done with it.

Final Debriefing

What did I learn?

From Here


fin

I hope you enjoyed.
If interested in more:


My Main Page
www.paufler.net

Coding Home Page
Brett Code


paufler.net@gmail.com

Terms of Service
© Copyright 2016 Brett Paufler