Numpy Test Pattern: Mandelbrot
Sort of a 'Hello World' for Numpy.
Sort of beyond that.

Zeroing-In on the Mandelbrot Set
Function automatically zooms in on the most interesting quadrant (where the number of black pixels is most equal to the number of white pixels -- i.e. a 50-50 split).
Second iteration (or is that the third, suppose it matters how one counts) and all is well.
First break. Once again, this is due only to the picture size (and hence the individual pixel values calculated).
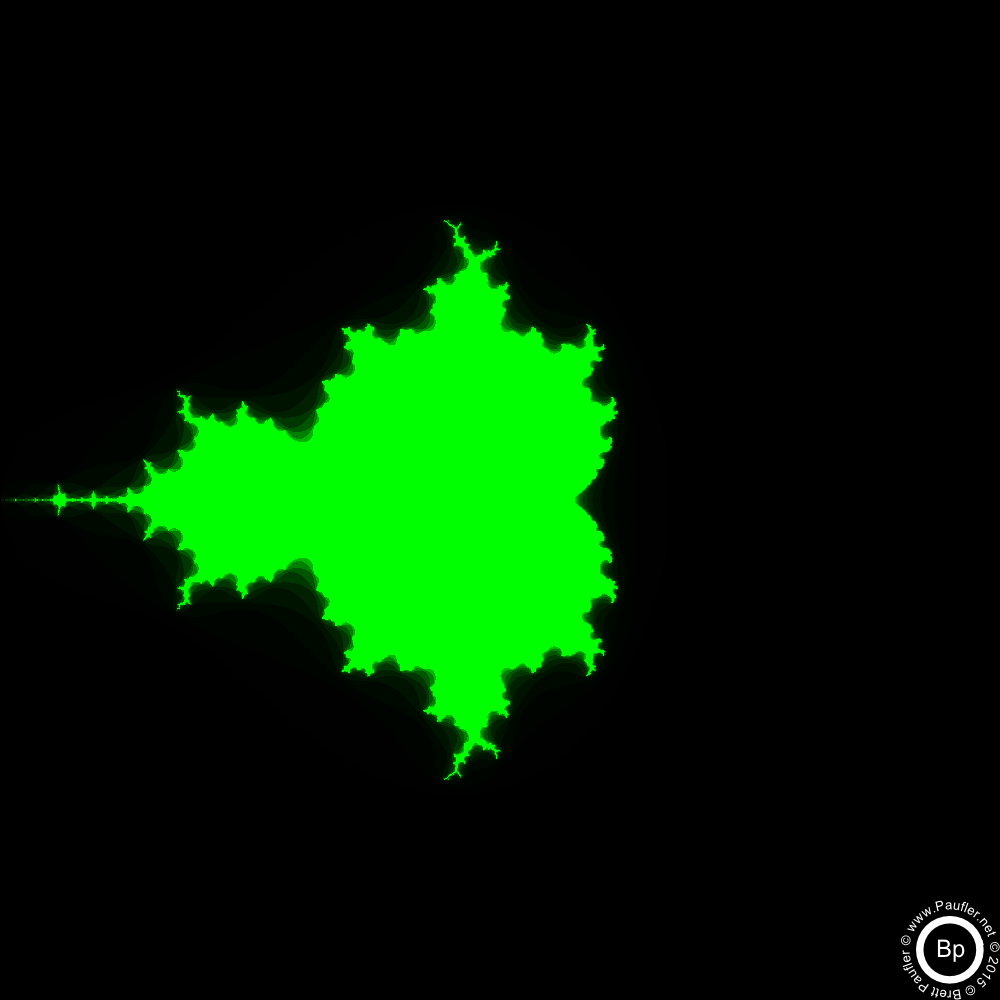
White is the mandebrot set.
The iteration (x22 + c) tends toward infinity in the black area.
Second break (divergence). 'Tends toward infinity' means (x22 + c) is greater than 2 after 50 iterations.
If you don't already understand the Mandelbrot Set, the previous is extremely unlikely to shed any additional light.
Final divergences: all four resolution paths are now drilling down ever deeper into different regions of the Mandelbrot set.
The self similarity is still easy enough to see (to me, anyway).
Here the lines start to smooth. This is a limitation of Numpy's resolution (or a limitation of my ability to tweak Numpy, take your pick).
Numpy only has 15 digits (or whatever, can't say I checked or care) of resolution.
So, at the end of the line, there is no variance in the values.
And we're looking at the blurriness inherent in 15 digits (or whatever) of accuracy.
Or maybe there's some other explanation beyond my ken.
Don't ask my why the 500px blurs out slightly ahead of the 1000px series. Probably just luck of the draw (e.g. where the last significant digit lands).
Resolving the Mandelbrot Set

All those colourful pictures of the Mandelbrot Set?
They're based on what pixels tend toward infinity (are greater than 2) at each level of iteration.
This is the base iteration:
def base_iter(x,c):
return x*x + c
So, like a sculptor, higher resolutions narrow the field.
There is a point of diminishing returns.
And then, as much as I'd like to push 10,000px images to the web, as of 2015, modern browsers just aren't up to the job yet. Give 'em a year or two.
Computing the Mandelbrot Set in Python
Code be code.
And this be the code.
#Copyright Brett Paufler
#Released Under the Exclusive
#For Information Purposes ONLY (ALL RIGHTS RESERVED) License
import numpy as np #because that's how the cool kids do it
import skimage.io
def base_iter(x,c):
'''This is the Heart of solving the Mandelbrot Set
Full numpy arrays will be fed into this function
'''
return x*x + c
def main_iter(c,numIt=50):
'''Returns the Mandelbrot Set
c is a numpy array of complex numbers defined over
the area of interest
numIt is the number of iterations, more, better
but there is a point of diminishing returns
'''
#This x (and this c) are conceptually the same,
# as per base_iter above
x = np.zeros_like(c)
for _ in range(numIt):
x = base_iter(x, c)
#If the absolute value of (a+bi) ever exceeds 2
#The point is not part of the Mandelbrot Set
#And tends toward infinity
x = abs(x)
x[x>2] = np.nan #Most of these values are already np.nan
x[x<=2] = 1
x[np.isnan(x)] = 0
return x
def i_coord(s, (uL,lR)):
'''returns a complex coordinate grid (aka c in the above)
size = (s,s) = s high, s wide
min_max is passed in a tuple of two complex numbers
uL is the min (Upper Left)
lR is the max (Lower Right)
Odd fact, I am right/left dyslexic
Often heard around my house,
'No! Your other right!'
'''
#real part, as a row
r = np.linspace(np.real(uL), np.real(lR), s, dtype=complex)
#imaginary part, as a column
im = np.linspace(np.imag(uL), np.imag(lR), s, dtype=complex)
im = np.reshape((im * 1j), (s,1)) #turns into a column, essentially
#add a row and a column together in Numpy
#get a Matrix, row wide, column high
return (r+im)
def next_coor(s, mandebrot, c):
'''Returns the area of 'Most Interest' in the Mandelbrot Array
Most interest being defined as relatively even numbers of 0's & 1's
s = size (s,s) of image out, as it does everywhere else
mandebrot (misspelled, of course) is the picture image array
c is the starting complex array (for this go round, this image)
'''
#t being the value of 50-50 0's & 1's
t = s*s/8.0
m = []
#This is messy
#It's the type of hell that's usually easier for me
# to rewrite than debug
m.append((abs(t - sum(sum(mandebrot[:s/2, :s/2]))),
(np.min(c[:s/2, :s/2]), np.max(c[:s/2, :s/2]) )))
m.append((abs(t - sum(sum(mandebrot[:s/2, s/2:]))),
(np.min(c[:s/2, s/2:]), np.max(c[:s/2, s/2:]) )))
m.append((abs(t - sum(sum(mandebrot[s/2:, :s/2]))),
(np.min(c[s/2:, :s/2]), np.max(c[s/2:, :s/2]) )))
m.append((abs(t - sum(sum(mandebrot[s/2:, s/2:]))),
(np.min(c[s/2:, s/2:]), np.max(c[s/2:, s/2:]) )))
#sort, take the first (lowest t-sum),
# return the second part of the tuple
m.sort()
_, (min_max) = m[0]
return min_max
def auto_zoom(s, n, min_max=(-2.0 +2.0j, 2.0 -2.0j)):
'''Successive Mandelbrot's with Magnification
s = image size
n = number of successive images (blurs out at 20 or so
min_max is the starting area of interest
for a bunch of size options (20 images each)
for s in [100, 250, 500, 1000]:
min_max = (-2.0 +2.0j, 2.0 -2.0j)
auto_zoom(s,20,min_max)
'''
#1 loop per image out
for n in range(1,n):
print "\nStarting Loop"
print "Min Max: %d, %r" % (s, min_max)
c = i_coord(s, min_max) #c array for current coordinates
mandebrot = main_iter(c) #the main computation
sN = "mandebrot_{:0>4}_{:0>4}.png".format(s,n)
print "Saving %s" % sN
skimage.io.imsave(sN, mandebrot) #save the image
min_max = next_coor(s, mandebrot, c) #reset coordinates
def main_seq_picture_iter(s,
numPics=12,
min_max=(-2.0 +2.0j, 2.0 -2.0j),
intermediate=True):
'''saves a series of images,
whereas autozoom focuses in (drills ever deeper)
into the Mandelbrot Set,
This function outputs a series of ever refined images
focusing on a single area of the set
s = size of pictures to save
numPics = number of sequential images
(iterations, refinement of the Mandelbrot set)
min_max is tuple of area of interest
so by manually (or by other means)
the images may be obtained for any section of the set
intermediate = whether to save the 'part way' image progressions
(rather than just the final product)
Probably rather than a function call,
one should think of this as a script.
It solves a problem (pictures for this webpage).
But to solve another problem,
it would need to be rewritten or tweaked
(and not just passed different parameters)
'''
#c = array of complex numbers
#target of Mandelbrot image area
c = i_coord(s, min_max)
#g = for the compound image out
# green and grayscale
g = np.zeros((s,s))
#x is the incremented array
# the increased resolution copy of the Mandelbrot set
# as per other functions above (same x, essentially)
x = np.zeros_like(c)
for n in range(1, numPics + 1):
x = base_iter(x, c)
#p = binary (black/white) (0,1)
# color scale image for each iteration
# Note the logic, similiar to main_iter()
p = x.copy()
p = abs(p)
p[p>2] = np.nan
p[p<=2] = 1
p[np.isnan(p)] = 0
#increments the soft output, grayscale array
# Since this is an image effect
# p*n, p+n, p by itself, whatever
g += p * n
if intermediate: #save a PNG
sN = "mandebrot_resolve_{:0>4}_{:0>4}.png".format(s,n)
skimage.io.imsave(sN,p)
print sN
#After the Loop, Output some Compound Images
z = np.zeros_like(g, dtype=int)
o = np.ones_like(g, dtype=int) * 255
sN = "mandebrot_full_resolve.png" #white circle, gray Mandelbrot
skimage.io.imsave(sN,g) #one layer, so grayscale
sN = "mandebrot_full_resolve_green.png" #green circle
skimage.io.imsave(sN,np.dstack((z,g,z,g))) #(R,G,B, Alpha)
g = g / np.max(g) * 255
print np.max(g), np.min(g)
g = np.array(g, dtype=int)
sN = "mandebrot_full_resolve_green_%s.png" % s
skimage.io.imsave(sN, np.dstack((z,g,z,o))) #not used
print sN
sNa = "mandebrot_full_resolve_green_alphatrack_%s.png" % s
skimage.io.imsave(sNa, np.dstack((z,g,z,g))) #Green Mandelbrot
print sNa
return s
main_seq_picture_iter(1000, 12)
'''
Originally, I had it on my TODO list to do a colourized version
of the Mandelbrot Set (Using some sort of compound logic),
but I'm not convinced the colours mean anything (are just random),
so I've sort of lost my enthusiasm for the project.
Still, someday...
'''
Code as Text File: mandelbrot_numpy.txt
And that's all I have to say about that...
(famous last words)
More Coding Related Stuff
paufler.net@gmail.com
Terms of Service
© Copyright 2015 Brett Paufler










































































